Ricardian Intensive Land Rent As The Origin of Marginal Analysis
Note: Apologies for the lack of some subscripts. Substack does not support math
To some extent, the historical development of economic thought interests me. In particular, the reason for the move from classical economics to a modern economics due to the marginal revolution is the topic that has piqued my interest. Based off readings of Fabio Petri, I was inspired to make this relatively short post to answer this very question.
The vulgar answer to this question from Austrian and affiliated think tanks is “the common sense reasoning that value is subjective to the individual”. Often times the paradox of value is brought up as well to throw scarcity into the mix. This misguided analysis can be ignored entirely for it confuses value as used in an economic sense with value of an axiological definition, when an axiological objectivism of value is not what the classical long period approach to value and distribution holds to. The relatively more intellectually honest explanation(strong emphasis on relatively) is that through using utility as a standard of value and hence adopting an exchange oriented approach to the economy, the problematic classical long period approach could be replaced with a coherent marginalist long period approach.1 Austrians who reject marginal productivity theory and Pareto efficiency conditions however are yet to develop a formalized subjective theory of value apart from the formal capital theoretic work that builds off of Bohm-Bawerk.2
How is the origin of marginalism as a solution to the problems faced by the classicals at the time to be explained then? Ricardo’s theory of intensive rent, generalized by Von Thunen to apply to all factors and not just land, is where the answer may lie. This explanation may seem counter intuitive at first so it is best to explain intensive rent.
To put it short, assume a fixed quantity of land with uniform quality. When that land is underutilized, rent will not exist as supply is more than enough to fulfill all producer demand for land. However, when the demand for land exceeds supply and there exists a choice between two methods of production, due to competition rents will emerge as to make the profitability of each method equal. At this level of rent, both methods coexist, with the more productive one gradually taking over more units of land in production. Intensive rent is the rent that emerges due to competitive forces in order to make two different methods of production equally profitable, albeit at a lower rate of profit than originally.
Now lets use the logic of intensive rent to see how the marginal product of capital can be derived. Corn is produced as a consumption good and is also utilized as capital in the form of seed. Assume that the supply of land T is unity, T=1. Let 𝝺1 be the technical coefficient for capital in method 1. Let t1 be the technical coefficient for land. The price p1 is set to unity, giving us:
Where r is the rate of profit and 𝛽 is rent. It is important to note that the price described is not a spot price. It can be treated as a long run one merely for the sake of analysis. When land is underutilized, rent is 0. Let q1 be total output when land is fully employed. Given T, output is:
when land is fully employed. The amount of capital employed at this point is K1. Let K1 be:
When land is underutilized, this is also the slope at which the amount of capital utilized increases for each additional unit of land utilized in production, which is equal to (1+r) due to the absence of rent. For output to expand past q1, a more productive method must now be introduced. Lets call this method 2. However, because land is already fully utilized, intensive rent emerges. 𝛽 rises due to competition in order to render both methods equally profitable.
Now the rate of profit r is lower than it was previously. Both methods are utilized in production, with the method 2 gradually replacing method 1 in the production of corn. The rate at which output increases is thus
Both terms are equivalent to q2 and q1 respectively. Now we can calculate the marginal product of capital by dividing the change in output above by the rate of change in capital utilized K2 - K1, where K2 is the amount of capital utilized when method 2 completely replaces method 1. Starting from the left, we get:
From the price equations shown previously, we can derive the equation for rent and by substituting that into the price equation for method 2(remember that both prices are equal to 1) we prove that (1+r) is equivalent to the expression on the furthest right side of the equation above. This is the gross marginal productivity of capital given the simultaneous usage of methods 1 and 2. However, this value of r is smaller than the value of r when only method 1 was utilized in production. The value of r when only method 1 was utilized can likewise be treated as the marginal productivity of capital when K=K1. Hence after the introduction of method 2 to expand production beyond q1 despite fully utilized land, marginal productivity has decreased.
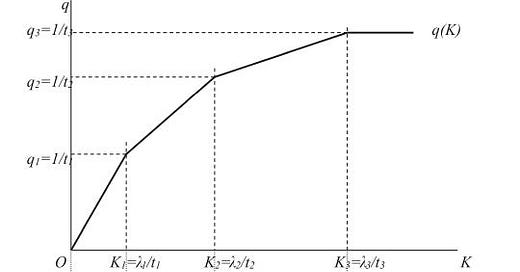
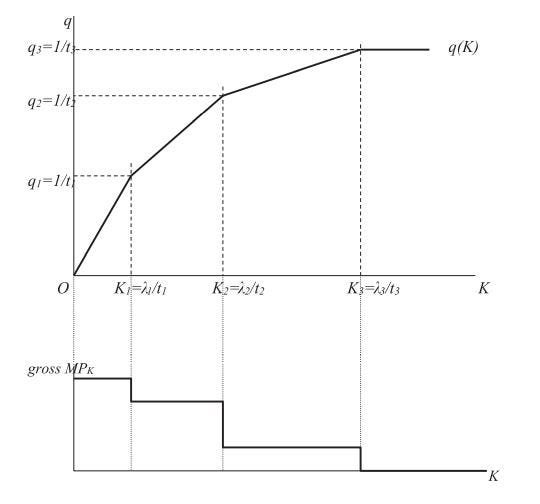
The same logic is expected to hold for expanding production beyond q2 through the introduction of a method 3. As production expands and the new method gradually replaces the old method, we see diminishing returns to productivity. This can be graphed as a standard production function with K on the abcsissa and q on the ordinate
Each kink on the graph represents a point where one method prevails. The slope of each segment is the marginal productivity of capital as one method slowly replaces another. Add an infinite number on methods and kinks vanish entirely, each point on the graph represents a new superior method that is more capital intensive and land saving. In other words, by rendering the graph continuous with infinite methods, direct factor substitution can be shown to exist between capital and land.
The same logic applies if we treat capital as the fully employed factor of production and land as variable. In this case we are also able to derive the marginal productivity of land. With labor and capital, by holding one fully employed, we can get the marginal product of the other subject to diminishing returns. This is the generalization of Ricardian intensive rent mentioned at the start. The generalized theory of intensive rent allowed for the explanation of direct factor substitution and hence the explanation of factor incomes as based upon marginal products. As one could also notice, this approach also provided the rationale for full employment of resources in the long run assuming constant returns to scale.
A marginalist long period approach explains factor payments through supply and demand via factor substitution mechanisms, both technical(variability of the K/L ratio through choice between infinite techniques) and indirect(through changes in demand reflecting changes in derived demand for products). The long run is associated with fulfillment of Pareto Efficiency conditions on both production and exchange sides hence utility being maximized, prices being equivalent to the minimum average total cost, and factors being paid their marginal products.
See Lewin, Cachanovsky, Hulsmann, Fillieule, et al



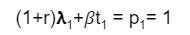
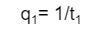

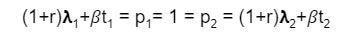
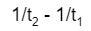
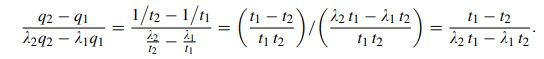
This you Mr."@Paradox00760811"
https://youtu.be/QI41JLc2Oc0